page30

Theory - Linked lists

What now seems way back on page 25, linked lists were mentioned with a promise that they would be covered later, well it's now later. A re-cap on the problems with arrays may be needed though at this point to justify why linked lists are so very useful.

When arrays were covered, two problems with them were highlighted :

The size has to be set at program design time
- When information is being stored in an array, the size of the array ( number of elements ) has to be specified in the program code. So, for example, if you were holding school marks, with each student in the school having an array entry, you would need to declare the size of the array ( in the program code ) to contain the same number of elements as there are students. This leads to problems though, because the number of students in a school changes all the time, new students arrive, students drop out etc.. The only way around this problem is to declare the array larger than the number of students and have a variable holding the number of students ( so you can work out the final array element in use ). This means though that there will always be, probably a large amount of array elements unused, also, removing a student is difficult as well. Page 25 showed a way around this problem, by not using arrays but using dynamic memory allocation to declare the size of the memory block at run time. This still though, didn't elminate the second problem below :

Arrays are allocated as single continuous blocks of memory
- There may be cases where there is enough free memory available to store an array, but there isn't a block of continuous memory available, in other words, the memory is fragmented. This is very unlikely though with PC's and Windows nowadays, but storing data continously in memory has another drawback, whether this is stored in an array or a large dynamically allocated memory block. This problem occurs if you want to sort or store the data in any type of ordered way. To sort an array into order involves moving data to different places in memory, which in computer terms is slow, it is a lot better to move the order of the data, without actually moving the data itself. This may sound a bit confusing now, but all, hopefully, will become more obvious with linked lists.

Linked lists solve these two problems, but add yet another problem, in that there is no automatic support for linked lists built into compilers. They are probably best described as a technique, instead of a language feature ( like arrays ). This means that the programmer has to do the work in setting them up and organising them, which is a bit confusing.

Linked lists - description

A linked list is a dynamic data structure, which means that the memory to hold the data is created at run time ( dynamic ), and stored in a structured way ( data structure ). The items in a linked list do not have to be stored in contiguous memory locations like an array. Each item in the list is called a node, which contains data as well as a pointer to the next node in the list ( a link pointer ). Normally there is only one variable that is associated with a linked list, which is a pointer variable to the first node in the list. From this point, the links in the list can be followed until the desired node is found. 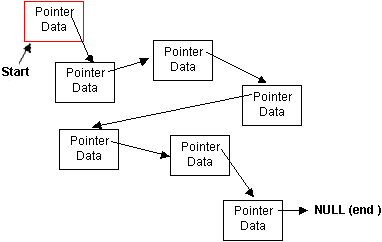The last node in the list doesn't point to another node, but points to NULL, indicating the end of the list. The diagram below shows this a lot better than this expanation :

In the diagram, each node is shown in the rectangles and contains a pointer to the next node in the list ( shown by the arrows ), and a data portion which holds the information for the node. The nodes are deliberately drawn in the diagram in a hap-hazard way to show that each node can exist in any portion of memory, not necessarily adjacent to or even close to the neighbouring nodes in the list. The start of the list is also shown, which is just a pointer to the first node. From this start pointer any node can be referenced, for all but the first node though, other nodes will have to be "passed through" to get there. The end of the list is indicated by the final node pointing to NULL.

Normally, when a linked list is initialised, the start pointer will hold NULL to indicate that the list is empty, but as soon as a node is added to the list, this changes. The basic operations on a linked list are to add nodes and delete nodes :

Add - You have to have the ability to add a node to the list, this is normally added at the start of the list, but in effect you can code it so that it is added anywhere you like.

Delete - The ability to delete any node from the list is also needed, and generally is a lot more difficult to implement than adding a node. You can have double linked lists, which do help with deleting a node, but make adding a node more complex. A double linked list is where each node has a pointer to the next node, and also an additional pointer to the previous node.

These two basic operations are explained below. There are a number of ways of implementing these operations though, but i'll try to keep this as simple as possible for this.

Operations on linked lists

Adding a node to a linked list

Adding a node isn't to difficult, but can be depending on how you implement the list. With a simple single linked list, and not needing to worry about the position in the list the new node is added, it is a really easy task to add a node. This is done to the start of the list, as shown in the diagram below :

The red node indicates the new node and the process involves :

Dynamically create the memory for the new node

Set the link pointer of the new node to equal the start pointer

Set the start pointer to point to the new node.

Deleting a node from the list

Deleting a node from a linked list is a lot harder than adding one, this is especially true in the case of a single linked list as is being used here. The problem is that the link from the parent node has to be set up to point to the child node of the node being deleted. In other words, the link from the node before the node that is being deleted has to be changed to point to the same link as the one being deleted points to. The nodes don't hold information on there parent nodes, just child nodes, which is why it requires more work. The diagram below shows the state of the list after the node in red is removed.

The process of deleting a node involves :

Find the node to be deleted, remembering the previous node as the list is traversed through

If the previous node is the start, set the start to be the child of the node being deleted

... otherwise ... set the link from the previous node to point to the same link as the node being deleted points to

Free up the memory for the deleted node.

Summary

Linked lists aren't easy to understand at first, so don't be worried if it's not all clear. The program on the next page will help understand them a lot better, you may want to skip on to the next page and then come back here after seeing the code. The one thing for sure though, is don't pass over linked lists because they appear difficult. They're important to understand, especially if you write programs that are expandable ( ie with addon's ).

This page showed the theory behind linked lists, but it is the actual code that will be the key. There are a lot more operations on linked lists that are not shown here, but they will be implemented in the sample program next.